Friday, 6 May 2016
Rente ricardienne et règle dHotelling comment un économiste classique voit les ressources naturelles

Et pourtant, les économistes classiques, à l'image de David Ricardo, ont longtemps regardé cette question de haut. Il a fallu attendre le XXe siècle et Harold Hotelling pour voir s'ébaucher une théorie néoclassique des ressources épuisables. Voyons ce qu'ils ont à vous dire...
Exploitez dès que les coûts d'extraction sont inférieurs au prix du marché (Ricardo)
Quelque part dans le grand livre des manques d'intuition des pères de l'économie trône cette citation fameuse de Jean-Baptiste Say :
 Les richesses naturelles sont inépuisables, car, sans cela, nous ne les obtiendrions pas gratuitement. Ne pouvant être ni multipliées ni épuisées, elles ne sont pas l’objet des sciences économiques."
Les richesses naturelles sont inépuisables, car, sans cela, nous ne les obtiendrions pas gratuitement. Ne pouvant être ni multipliées ni épuisées, elles ne sont pas l’objet des sciences économiques."Pour les premiers économistes, dont Say, l'idée même de ressources épuisable est obscure. En effet, malgré le début de la révolution industrielle, la terre est encore de loin la ressource naturelle la plus critique. Il n'est donc pas surprenant que lorsque David Ricardo parle des ressources minières (dans Des principes de l'économie politique et des impôts en 1823), il utilise le même raisonnement que pour décider de cultiver ou non un terrain, oubliant au passage le caractère non-renouvelable de ces ressources.
Le principe proposé par Ricardo est le suivant : A un instant t, vous pouvez vendre votre ressource au prix du prix du marché (appelons-le p(t), comme prix) à condition de l'extraire, ce qui a un coût (c(t), comme coût). Vous allez donc gagner (ou perdre si le coût d'extraction est supérieur au cours de la ressource) p(t)-c(t). Cette différence définit le prix de la ressource en terre que l'on note λ(t).
Pour Ricardo, vous avez intérêt à extraire votre ressource dès que λ(t) est strictement supérieur à zéro, c'est à dire dès que le prix d'une unité de ressource est supérieure au coût de son extraction.
Prendre en compte la valeur future de la ressource (Hotelling)
Il y a quand même un petit défaut dans ce raisonnement : comme votre ressource ne se reconstitue pas, vous avez certes gagné λ(t) en l'exploitant mais vous avez aussi définitivement perdu l'opportunité d'attendre un temps x et de gagner λ(t+x).
Si λ(t+x) est inférieur ou égal à λ(t), tout va bien pour vous. Mais a priori ce n'est pas le cas : on peut supposer que les coûts d'extraction vont décroitre avec le progrès technologique et que le prix de la ressource va augmenter au fur et à mesure qu'elle devient plus rare, donc que la fonction λ est croissante.
Est-ce que cela signifie qu'il faut toujours attendre avant d'exploiter une ressource ? Pas nécessairement, mais cela signifie deux choses importantes par rapport à la règle de Ricardo :
- Que la décision d'exploiter ou non une ressource n'est pas basée uniquement sur la situation actuelle mais aussi sur la situation (cours, progrès technologique, etc.) que vous anticipez dans le futur.
- Que vous ne devriez exploiter votre ressource non-renouvelable que s'il est plus intéressant pour vous d'obtenir une somme λ(t) maintenant plutôt que d'attendre un peu et d'obtenir une somme a priori supérieure λ(t+x).
En 1931, le statisticien américain Harold Hotelling a consacré un long article à ce sujet. Pour lui, décider d'extraire ou non une ressource revient à choisir entre :
- Laisser en terre la ressource pendant un temps x afin de gagner λ(t+x)
- L'extraire et la vendre immédiatement avec un profit λ(t), puis placer ce profit avec un niveau de risque comparable à celui de laisser votre ressource sous terre et obtenir un taux d'intérêt γ de telle façon que, avec les intérêts composés, votre gain au bout d'un temps x sera :

Derrière cette formule un peu barbare se cache une idée toute simple. Mettons que le pétrole que vous avez découvert dans votre jardin puisse vous rapporter 100€. Vous pouvez extraire et placer cette somme sur votre livret A (disons à 2%) et vous aurez 102€ dans un an, vous n'avez donc intérêt à attendre que si vous pensez que votre réserve de pétrole vous rapportera au moins 102€ l'année prochaine. C'est ce qu'on appelle la règle d'Hotelling.
Si vous décider de gérer votre ressource en vous appuyant sur la règle d'Hotelling, cela a deux conséquences intéressantes (surtout pour analyser la situation actuelle du marché du pétrole) :
- Cette règle implique que les cours des matières premières devraient être corrélés aux taux d'intérêt.
- Elle signifie aussi qu'une baisse des cours peut être auto-réalisatrice : si les propriétaires de ressources naturelles anticipent que la hausse des cours ne va pas être suffisante, ils ont intérêt à extraire le plus vite possible et à placer leur argent ailleurs... ce qui aura pour conséquence de faire effectivement baisser le prix de la ressource (et d'amener d'autre exploitants à revoir leur prévisions à la baisse et ainsi de suite : le phénomène peut s'auto-entretenir).
Alors qu'allez vous faire des richesses enfouies dans votre jardin ? Vous pouvez continuer votre réflexion avec ces articles :
- Combien d'années de pétrole ? Et autres questions sur les stocks de ressources non-renouvelables
- Comprendre ce que sont les externalités positives et négatives : définition et exemples
- L'actualisation, obstacle majeur à l'évaluation économique de l'environnement
Publié le 19 février 2015 par Thibault Laconde
Labels:
Ãconomiste,
classique,
Comment,
dHotelling,
et,
Les,
naturelles,
rÃgle,
Rente,
ressources,
ricardienne,
Un,
voit
Subscribe to:
Post Comments (Atom)
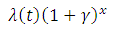
No comments:
Post a Comment